rpnjcalc manual
rpnjcalc is a RPN calculator implemented in javascript and
html. It is platform independent and requires only a javascript
capable webbrowser.
RPN stands for Reverse Polish Notation. Reverse Polish
Notation was developed in 1920 by Jan Lukasiewicz as a way to
write a mathematical expression without using parentheses and
brackets.
Why should I use RPN?
- RPN saves time and keystrokes. You never have to account
for the parentheses while doing calculations. The process is
similar to the way you learned math on paper.
- You can see the intermediary results as you perform your
computations rather than just the answer at the end. This is
an extremely helpful byproduct. Math teachers are using this
feature to improve student understanding of mathematics
- An intermediate result allows the user to check the
results and correct errors more easily. It's easier to follow
the stream of calculation. The user defines the priority of
operators.
- RPN is logical because the user first gives the number
and then tells what to do with it.
- Because subexpressions are evaluated as they are entered,
entry errors are more obvious with RPN. On an algebraic
calculator, omitting an opening parenthesis, may not lead to
a calculation error until much later when an entire
subexpression is evaluated.
RPN is something that you will have to learn but once you
understood it and used it you will not use any other calculator
anymore.
RPN became popular through the HP calculators and there is
today a whole fan club around these HP calculators. Most HP calculators are collectors items
and are sold for very high prices.
See e.g http://www.hpmuseum.org/.
Unsing rpnjcalc
rpnjcalc is platform independent however the DOM/javascript
standard complience is not the same in all browsers. rpnjcalc
works with Mozilla, MS IE, Firebird and Opera. In Netscape 4 and
Konqueror the pure calculator works but the keyboard interface
does not work.
A very detailed explanation on how to use RPN can be found
at: http://www.hpmuseum.org/rpn.htm.
In short: You use RPN just like you have been told in school
when you manually resolved an equation on paper. You have the stack
(LIFO, last in first out, registers: X, Y, A, B, C) to store intermediate results. Let's take an example.
3 + 5
-----------
16 - (2 * 6)
You could start to evaluate this term at the numerator but
normally you would start with the more complex term, the
denominator, in this case. This is also what you do on an RPN
calculator:
Type: 2, enter, 6, *
You just calculated (2 * 6). Note that the numbers are entered
first and then you say what to do with them (* = multiply). You
see immediately the result in the display: 12
Continue with: 16, swap, -
You have just calculated: 16 - (2 * 6)=4. Now go to the
numerator.
Type: 3, enter, 5 +
You have now calcualted 3+5 and you have result form the
denominator (4) still in the stack at position Y.
Type: swap, /
... and you are done: The result is: 2
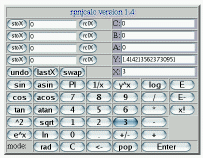
The specifics of rpnjcalc
You can either operate this calculator with mouse clicks or
you can use the keyboard.
However some web-browsers have keyboard shortcuts which may
conflict with the keys used by this calculator. Therefore you
need to place the mouse over the textarea below the calculator (click once,
the field will become dark gray).
The avaliable keyboard short cuts are documented in
the textarea. Numbers and all basic mathematical operators are
available as keyboard shortcuts.
More rarly used functions are only available as buttons
(click with the mouse). This is also to avoid that the keyboard
interface become too komplex to learn.
Function buttons:
- stoX -- store the value of X in the register next to the
stoX button for later use.
- rclX -- recall the value and write it to X
- undo -- undo one step
- lastX -- restore the last value of X
- swap -- swap X and Y
- mode:rad/deg -- switch between rad (sin PI=0) and deg
(sin 180=0)
- C -- clear X and write 0 into X.
- <-- -- delete the last digit of the number just
entered
- pop -- move the stack one evel down
- enter -- push the stack one level up
- E and E- -- this is to enter numbers as num*10^something
or num*10^-something
Real HP RPN calculators
rpnjcalc is very nice for occasional calculations but it is
nothing compared to a real HP calculator (such at the old
HP15c, HP42, HP48...). The precision of those HP calculators
is much higher than the mathematical precision that a web-browser
offers. HP calculators are also programmable which is not the case
for rpnjcalc.
Have fun with rpnjcalc but if you ever get
the chance to buy a real HP then don't miss it. I have really fallen
in love with my HP calculators and I still find the algebraic logic to be a bit lame. RPN is just a lot more elegant.
This rpnjcalc documentation was written by Guido Socher, guido
at linuxfocus dot org, Copyright: GPL
